- Brokers
- Employers
- Employees
- Solutions
- Benefits Administration
- Claims Administration
- Comprehensive Reporting
- Cost Management
- Customer Service
- Eligibility and Enrollment
- Financial Management
- Flexible Spending Accounts (FSAs)
- Health Care Networks
- Healthy Families Medical Center
- Cedar Health and Wellness Centers
- Health Management / Wellness programs
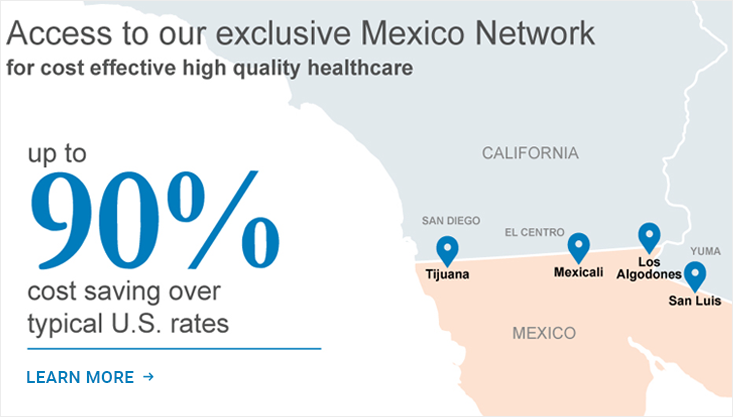
- Mexico Cross Border Program
- Pharmacy Benefits Management
- Stop-Loss / Reinsurance Solutions
- Technology and Efficiency
- Providers
- About
- News
- Contact

 Login
Login